Additive synthesis on a CPU and memory constrained ARM platform

The Korg Prologue and Minilogue-XD feature the ability to load digital user-oscillators that extend the range of possible sounds. Good candidates for these are emulations of oscillators from early digital/analogue hybrid synthesisers, replicating waveforms and wavetables from instruments such as the Korg DW-8000 , the Kawai K3 , the Ensoniq ESQ-1 and PPG Wave .

But, there is a catch. Logue plugins run on a relatively slow processor, an ARM Cortex M4, with only 32KiB of shared code and data space. In contrast, the DW-8000 uses 128KiB of ROM to store its waveform multi-samples, so replicating its waveforms by sample playback is challenging.

There is one existing DW-8000 emulation for the Logue that tries to do this, but the memory constraints mean that each waveform can use only a single short sample. The result is significant aliasing while the bandwidth of the waveforms is also compromised.

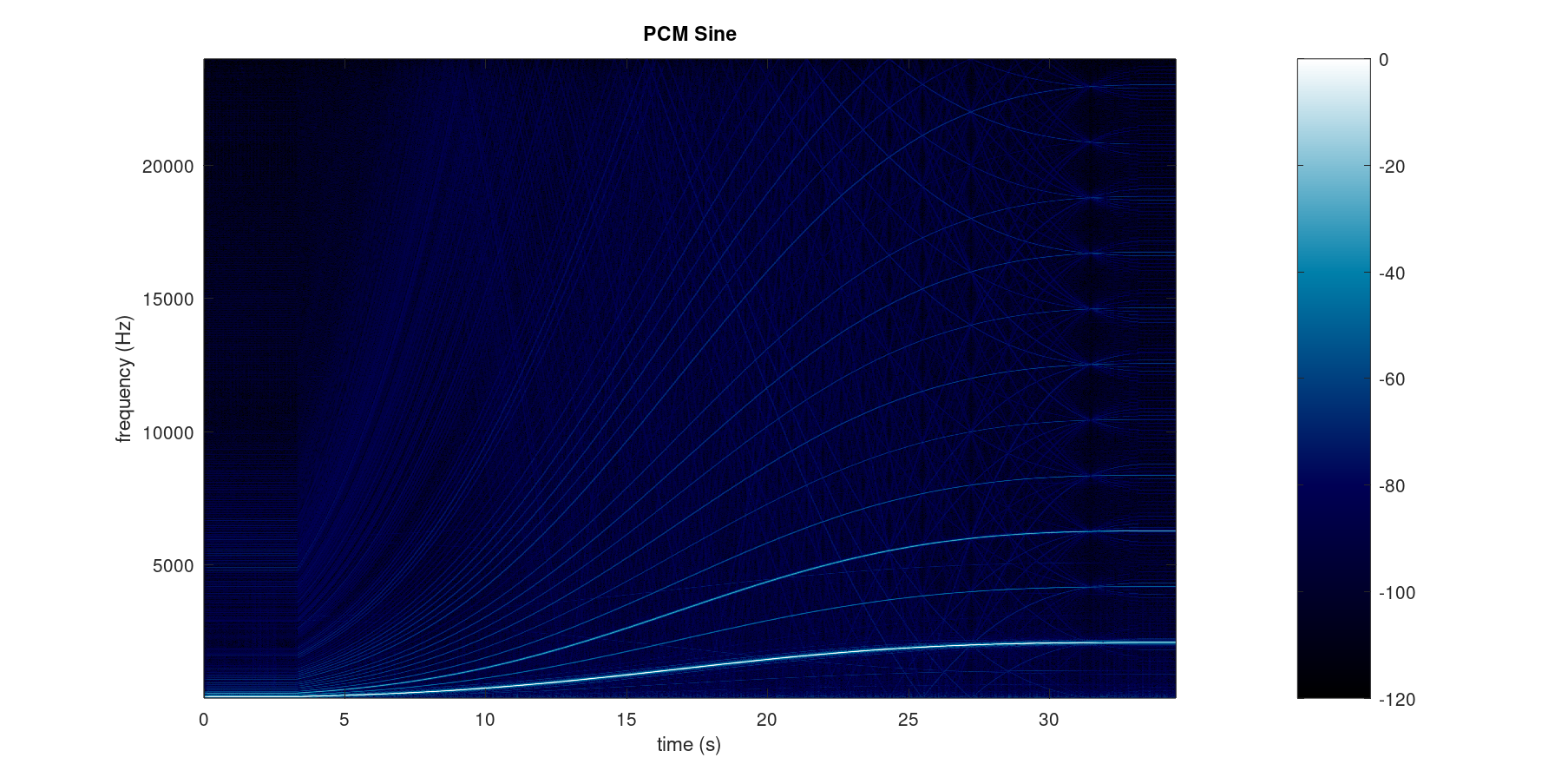
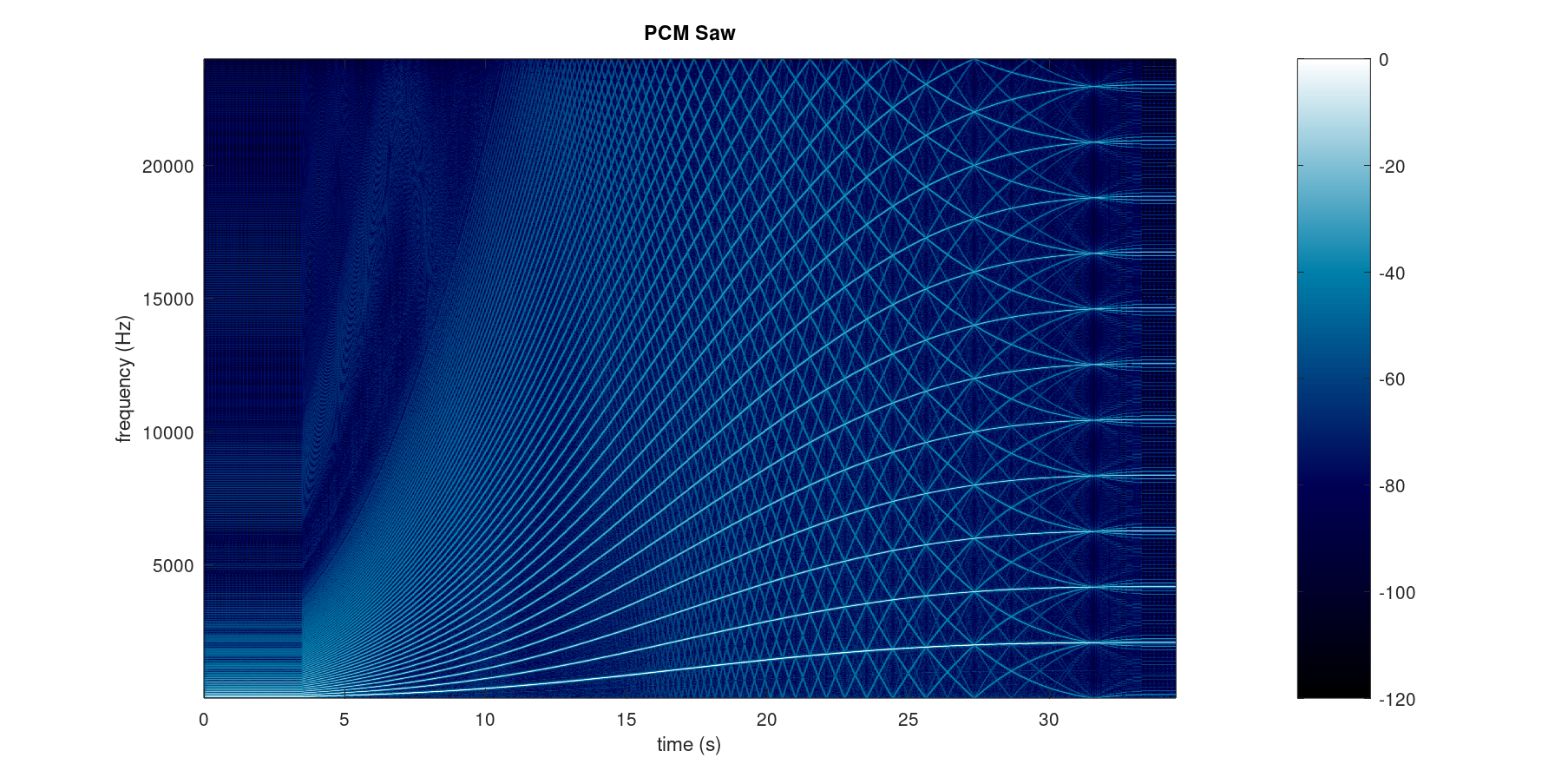
The following spectrograms ¹ show a 5-octave frequency sweep using the sine and sawtooth waveforms with this plugin (click the image to enlarge):

Even the sine wave shows significant additional harmonic content, while the sawtooth contains prominent aliased frequencies below the fundamental that sound like discordant whistles. In the upper octaves the aliasing is easily heard, while in the lower notes the sawtooth sounds duller than the original instrument. This is not an error in the plugin, but a limitation of PCM playback with constrained memory.

Logue plugins like fusion and phase7 use variations of the PolyBLEP family of algorithms. These works well for simple waveforms such as saw or square waves, but are difficult and computationally expensive to use with more complex waveforms such as are produced by wavetable interpolation.

A long standing alternative is to use Fourier synthesis to generate the waveforms - basically just adding up a bunch of sine waves with different amplitudes and frequencies. This is widely used in software instruments as well as hardware ranging from the classic synths such as the Kawai K5000 to modern designs such as the Novation Peak .

For the four viper plugins , two possible additive architectures were looked at: an overlapped inverse FFT and a brute-force bank of 128 sine-wave oscillators.

FFT approaches ought to give the most efficient implementation, but in this case it was not possible to achieve sufficient performance even with the optimised ARM CMSIS libraries. It turns out that although the Logue’s CM4 processor is clocked at 84MHz, 32 bit non-memory access instructions effectively run at half that rate due to the use of data memory to hold the plugin’s code. For example, the 16 bit Thumb-1 instruction “mov r0, r0” executes in 1 cycle, but the 32 bit Thumb-2 “mov r8, r8” requires 2 cycles. It is possible that custom assembler code that uses symmetries and simplifications in the IFFT input data could be used to gain sufficient performance, but it would be difficult to justify the development effort that would be required.

The alternative oscillator-bank approach, however, is trivially optimisable with inline assembler, and turns out to be capable of rendering waveforms with 128 harmonics in real-time - just enough to be useful.

Three different harmonic models were written using inline assembler with C macros for loop unrolling. The following assembly output shows the simplest of these models, under the assumption that all harmonics operate at a fixed integer multiple of the fundamental with synchronous phase:

ldmia	r2!, {r3, r4, r5, r6}           ; load eight 16 bit amplitude coefficients

lsrs	r7, r1, #19                     ; convert the oscillator phase angle to sine table index
subs	r1, r1, r0                      ; update the phase, ready for the next harmonic
ldrsh.w	r7, [r9, r7, lsl #1]            ; lookup the sine-wave
smlabb	r8, r7, r3, r8                  ; multiply-and-accumulate for the sine and harmonic amplitudes

lsrs	r7, r1, #19                     ; repeat for harmonic #1
subs	r1, r1, r0
ldrsh.w	r7, [r9, r7, lsl #1]
smlabt	r8, r7, r3, r8
...

lsrs	r7, r1, #19                     ; repeat for harmonic #7
subs	r1, r1, r0
ldrsh.w	r7, [r9, r7, lsl #1]
smlabt	r8, r7, r6, r8
...                                     ; repeat for the next block of 8 harmonics

The calculation is made in reverse order, with the highest order harmonics rendered at the start. Fully unrolling the code makes it possible to choose the maximum harmonic to be rendered, so that the simplest form of anti-aliasing can be trivially implemented by jumping to an appropriate start point in the unrolled code.

The harmonic amplitudes are specified by an array of signed 16 bit value, allowing good resolution. The use of signed amplitudes allows each harmonic to have an effective phase angle of 0 or 180 degrees. The restriction on the phase angle is largely a non-issue, as human hearing is very insensitive to harmonic phase. Curiously, it appears that both the DW-8000 and K3 waveforms appear to be constructed entirely from harmonics with the same restriction, suggesting that both waveform sets were generated algorithmically rather than sampled.

The code’s performance comes largely from the use of the ARM’s ldm instruction to load a block of 8 harmonic amplitudes into registers. A single Thumb ldr instruction takes 3 cycles to read a 16 bit value, but using the ldm amortises the memory access overhead so that the each 16 bit amplitude is read in less than a single cycle.

Calculating the phase of the harmonic uses repeated 32 bit addition. A shift operation converts this to a table lookup index for the sine wave, and a single ldr reads the sine value. The CM4 smlabb and smlabt instructions perform a 16x16 bit multiply with 32 bit accumulate, keeping a running total of the product.

A final performance gain comes from careful register choice. In particular, the subtract instruction for the phase angle can use a 16 bit Thumb-1 coding, saving one cycle compared to the Thumb-2 coding needed for higher register numbers. One cycle may not sound like much, but as this is done 128 times per sample it reduces the final CPU load by more than 7%.

With the above code, the execution time per harmonic, measured using dragon on a Korg Prologue, is 6.75 cycles. This is fractionally slower than the theoretical 6.625 cycles expected, likely due to infrequent memory bus contention from things like background DMA. This is theoretically just fast enough to render 256 harmonics at 48KHz, although practical implementations cap the harmonic count to preserve CPU time for other tasks ². In viper plugins, CPU is conserved either by dynamically apportioning harmonics between the two voices, or by using interpolation with a reduced sample rate.

The set of four viper plugins use several variants the above code, including a version with sparse harmonics (fewer harmonics in total, but each with an independent frequency offset), and a version that uses 8 bit harmonic amplitudes which can be smoothly blended to generate wavetable sweeps for the PPG Wave .

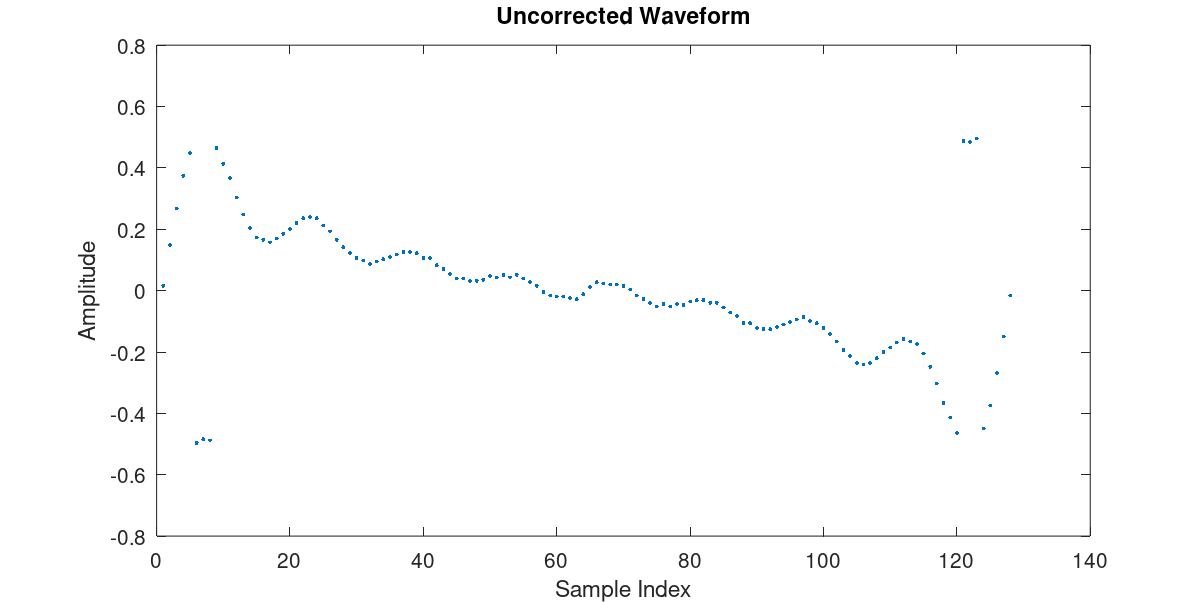
For each of the emulated instruments, an analyser was written that processes the original waveforms, converting them to harmonic form, selecting the appropriate model, and determining which multi-samples should be preserved (ie those with tonal changes that are not related to anti-aliasing). The analysers mostly rely on straightforward Fourier analysis, but in some cases more work was needed. For example, it turns out that some of the original PPG waves appear to contain numerical overflow errors, where amplitudes had exceeded the range of the 8 bit samples and wrapped:

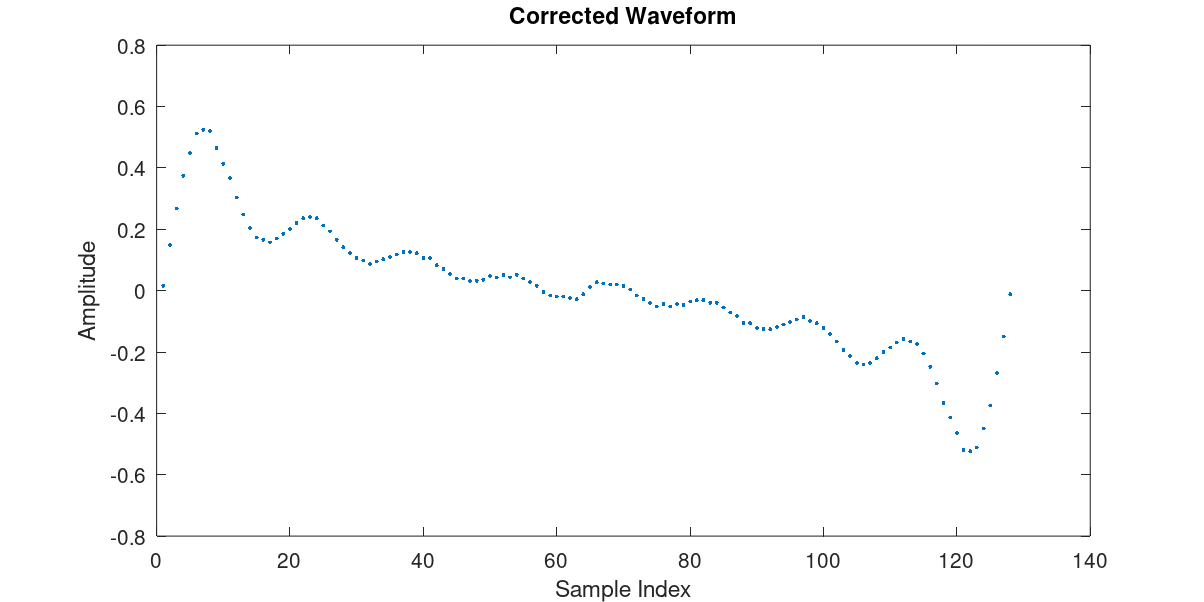
The PPG analyser detects and corrects these errors, restoring what was probably the intended waveform:

The errors appear to affect only some waves in a single wavetable (number 27 in viper-ppg). For authenticity, it is debatable whether these changes should be made or not, but the corrected waveforms sound much closer to the original intent (a formant sweep) and it is entirely possible that the errors might have been corrected in a different firmware version to that which was analysed.

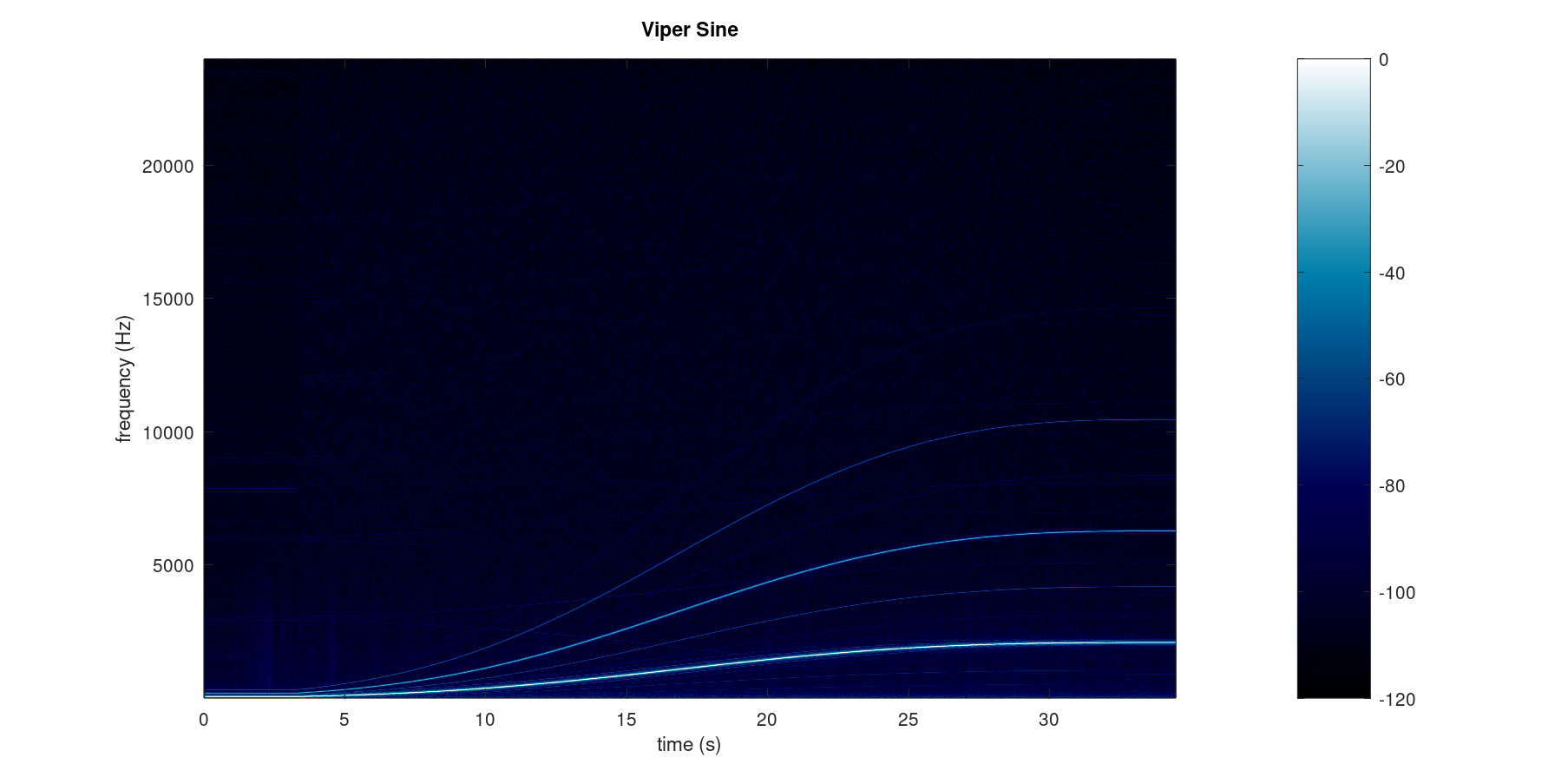
These are the spectrograms for a 5 octave sweep using viper-dw with the DW-8000 sine and sawtooth waveforms:

These show a huge improvement over the PCM playback example shown before, but are still not perfect:

• There is still some aliasing present, most visible with the 3rd and 5th overtones from the sine wave, and in the area close to the 24KHz Nyquist cutoff. More on this below.
• The brick-wall filter is perhaps a little too-sharp, and you can see some vertical noise spikes where the harmonics are cut. In principle this can be solved by rolling off the amplitude of the highest harmonics more smoothly, but this again needs more CPU time - and here the choice was made to use the remaining CPU for other features (auto-bend, noise generation, etc). These noise spikes are relatively low energy and at high frequency, and so are in reality inaudible.
• The limit of 128 harmonics means that base notes may be slightly duller than expected. In the sweeps, the lowest note is MIDI C2, which has a fundamental of 65Hz. This means that the highest harmonic possible here is at 8372Hz. Ideally a faster processor or potentially a more optimised (assembler) IFFT implementation could improve on this, but viper provides some mitigation by the use of different models. For example, some waveforms require only odd harmonics, so the highest harmonic can have double the frequency of the sawtooth shown here, while others are better modelled by a smaller number of harmonics but with greater flexibility over frequency.

The remaining aliasing comes from two sources. The first is the sine lookup table. To keep within the CPU budget it is not possible to use interpolation, so there is quantisation noise from the lookup process. To minimise this, the sine table is made as large as possible - fully half of the available memory in the case of the DW-8000 and K3 models. To do better than this would need either more memory or more CPU.

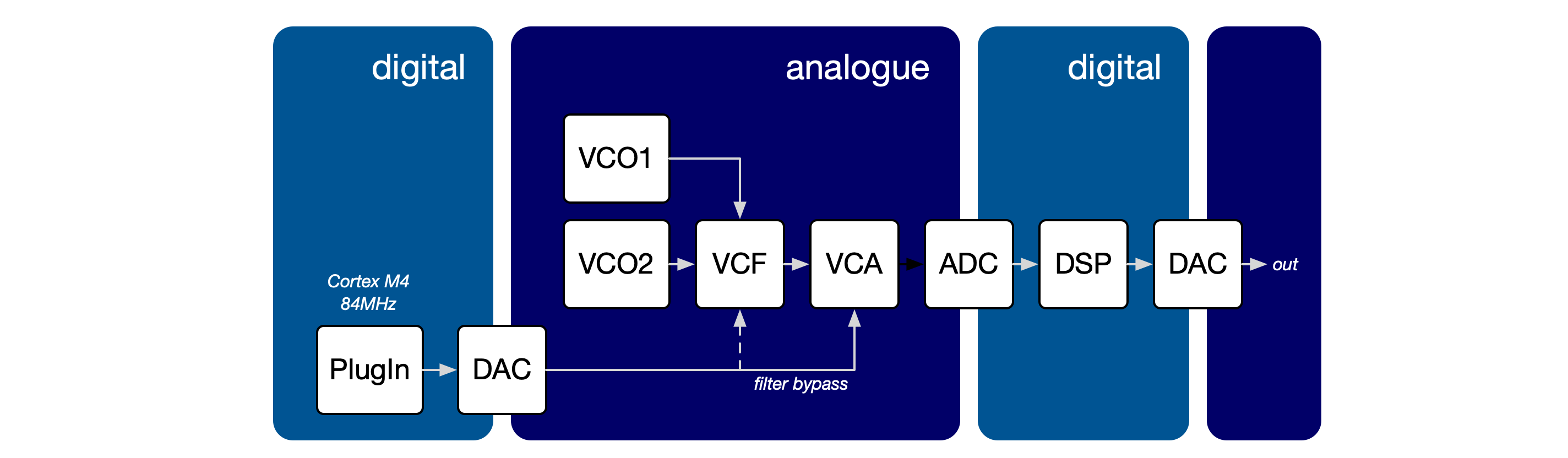
The second source of aliasing appears to come from the internal architecture of the Prologue synth:

After the Logue plugin has generated its digital output, this is converted to an analogue signal for mixing with the VCOs and subsequent processing by the VCF and VCA. This is then re-sampled in order to apply digital effects, before being again converted back to analogue for the final output. If these later stages induce aliasing or other harmonic distortions, we should be able to see that by looking at the output from the VCO.

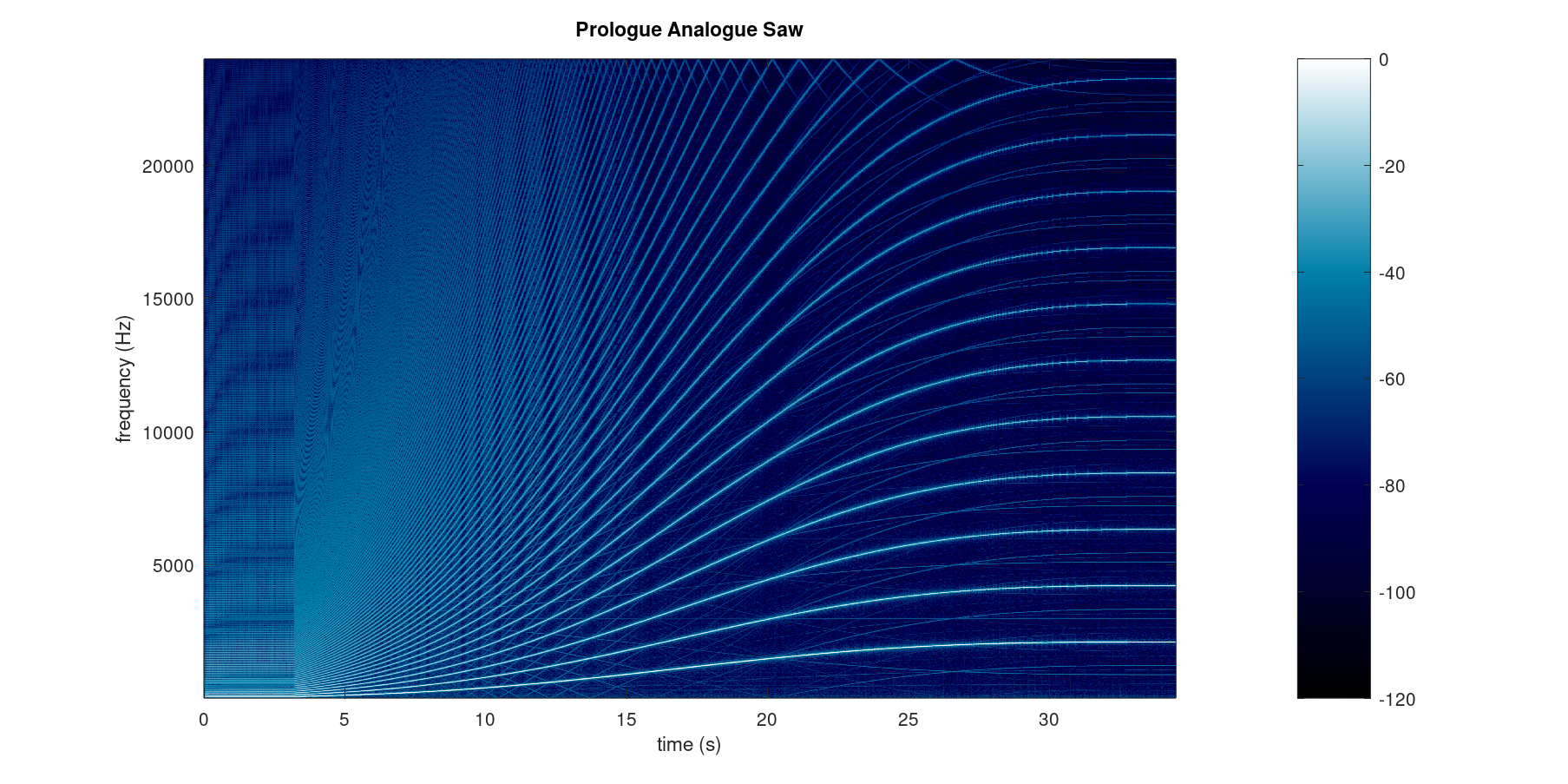
Here are the frequency sweeps using the Prologue’s own digital sine output (from the VPM) and a sawtooth from an analogue VCO:

Counter intuitively, the analogue sawtooth shows more artefacts than viper’s digital version, although in practice this is virtually impossible to hear.

Some of this likely comes from imperfections in the analogue circuitry itself, but some is inherent to the Prologue design where the analogue signals are subsequently processed by a digital DSP. A digital additive waveform generator can perform better than an analogue VCO because its digital brick-wall filter effectively leaves less high-frequency energy for the DSP ADC’s pre-sampling filter to reject.

Where the VCO wins, of course, is at very low frequencies - where viper’s maximum of 128 harmonics reduce the brightness of the sound compared to the analogue waveform. This is a limitation of the Logue’s CPU rather than the technique itself.

Overall, viper produces extremely accurate renditions of the original sounds, struggling only when the original samples contain large non-bandwidth limited transients. The PPG models are the most stressed by this, as the memory footprint limits the number of harmonics and the bit-depth of the harmonic amplitudes - and some of the waveforms appear to contain inadvertent numerical wrapping that would cause strong aliasing that is simply not possible to replicate with the available number of harmonics short of trying to deliberately clip the output waveforms. But the majority of waves are bandwidth limited and render accurately even with the limitations of the Logue platform.

PPG Original Waveforms	Viper Synthesised Equivalents

It is not clear where this will go next. The viper plugins probably push the current Logue instruments as far as they can go for PCM-like waveforms and wavetables. Importantly, the oscillators sound clean and musical and the primary limitations come from the speed and memory size of the Logue platform itself.

There remains one as yet unreleased variant that pairs a wavetable oscillator with a sweepable 128 band formant filter, roughly analogous to a pair of Kawai K5000 additive sources. However this still needs work to complete a graphical editor for the tables.